Multi-Sensor Fusion: LiDAR and Radar fusion based on EKF

[TOC]

Overview

• 代码：lidar_radar_ekf_fusion

System State Vector

$$x = [p_x, p_y, v_x, v_y]^T \in \mathbb{R}^{4 \times 1}$$

State Transition & Measurement Function

State transition function:

$$x^{\prime}=f(x)+\nu$$

Measurement function:

$$z=h\left(x^{\prime}\right)+\omega$$

其中，$f(x)$ 和 $h(x)$ 非线性，通过一阶泰勒展开可被线性化为

$$f(x) \approx f(\mu)+\underbrace{\frac{\partial f(\mu)}{\partial x}}_{F_{j}}(x-\mu)$$ $$h(x) \approx h(\mu)+\underbrace{\frac{\partial h(\mu)}{\partial x}}_{H_{j}}(x-\mu)$$

Kalman Filter Algorithm

State Prediction:

$$\begin{aligned} x^{\prime}_k &= F x_{k-1} + \nu_k, \quad u = 0 \\ P^{\prime}_k &= F P_{k-1} F^{T} + Q_k \end{aligned}$$

Measurement Update:

$$y_k = z_k - H x^{\prime}_k$$ $$S = H P^{\prime}_k H^{T}+R$$ $$K = P^{\prime}_k H^{T} S^{-1}$$ $$\begin{aligned} x_k &= x^{\prime}_k + K y_k \\ P_k &= (I-K H) P^{\prime}_k \end{aligned}$$

EKF Fusion Process

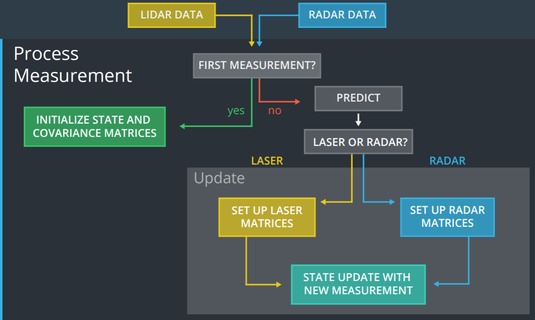
Initialization

• system state vector dimension: $n = 4$
• timestep: $t_0$
• system state vector: $x_0 \in \mathbb{R}^{4 \times 1}$
• process covariance matrix: $P_0$
• system state transition matrix: $F0 = I{4 \times 4}$
• process noise covariance matrix: $Q0 = 0{4 \times 4}$

Prediction

当前时间戳与上一测量数据时间戳的偏移（timeoffset）

$$\Delta t = t_k - t_{k-1}$$

状态转移方程

$$x^{\prime} = f(x) + \nu$$

2D常加速度运动模型 为

$$\left\{\begin{array}{l} {p_{x}^{\prime}=p_{x}+v_{x} \Delta t+\frac{a_{x} \Delta t^{2}}{2}} \\ {p_{y}^{\prime}=p_{y}+v_{y} \Delta t+\frac{a_{y} \Delta t^{2}}{2}} \\ {v_{x}^{\prime}=v_{x}+a_{x} \Delta t} \\ {v_{y}^{\prime}=v_{y}+a_{y} \Delta t} \end{array}\right.$$

写成矩阵形式

$$\left(\begin{array}{c} {p_{x}^{\prime}} \\ {p_{y}^{\prime}} \\ {v_{x}^{\prime}} \\ {v_{y}^{\prime}} \end{array}\right) = \left(\begin{array}{cccc} {1} & {0} & {\Delta t} & {0} \\ {0} & {1} & {0} & {\Delta t} \\ {0} & {0} & {1} & {0} \\ {0} & {0} & {0} & {1} \end{array}\right) \left(\begin{array}{l} {p_{x}} \\ {p_{y}} \\ {v_{x}} \\ {v_{y}} \end{array}\right) + \left(\begin{array}{c} {\frac{a_{x} \Delta t^{2}}{2}} \\ {\frac{a_{y} \Delta t^{2}}{2}} \\ {a_{x} \Delta t} \\ {a_{y} \Delta t} \end{array}\right)$$

抽象简写为

$$x^{\prime}=Fx + v$$

其中

$$v \sim N(0, Q)$$

State Transition Matrix

$$F = \left(\begin{array}{cccc} {1} & {0} & {\Delta t} & {0} \\ {0} & {1} & {0} & {\Delta t} \\ {0} & {0} & {1} & {0} \\ {0} & {0} & {0} & {1} \end{array}\right)$$

Process Noise Covariance Matrix

由上式

$$\nu= \left(\begin{array}{c} {\nu_{p x}} \\ {\nu_{p y}} \\ {\nu_{v x}} \\ {\nu_{v y}} \end{array}\right) = \left(\begin{array}{c} {\frac{a_{x} \Delta t^{2}}{2}} \\ {\frac{a_{y} \Delta t^{2}}{2}} \\ {a_{x} \Delta t} \\ {a_{y} \Delta t} \end{array}\right) = \underbrace{ \left(\begin{array}{cc} {\frac{\Delta t^{2}}{2}} & {0} \\ {0} & {\frac{\Delta t^{2}}{2}} \\ {\Delta t} & {0} \\ {0} & {\Delta t}\end{array}\right)}_{G} \underbrace{\left(\begin{array}{l}{a_{x}} \\ {a_{y}}\end{array}\right)}_{a} = Ga$$

根据 $v \sim N(0, Q)$

$$Q=E\left[\nu \nu^{T}\right]=E\left[G a a^{T} G^{T}\right]$$

因为 $G$ 不包含随机变量，将其移出

$$Q = G E\left[a a^{T}\right] G^{T} = G \left(\begin{array}{cc} {\sigma_{a x}^{2}} & {\sigma_{a x y}} \\ {\sigma_{a x y}} & {\sigma_{a y}^{2}} \end{array}\right) G^{T} = G Q_{\nu} G^{T}$$

$a_x$ 和 $a_y$ 假设不相关，则

$$Q_{\nu} = \left(\begin{array}{cc} {\sigma_{a x}^{2}} & {\sigma_{a x y}} \\ {\sigma_{a x y}} & {\sigma_{a y}^{2}} \end{array}\right) = \left(\begin{array}{cc} {\sigma_{a x}^{2}} & {0} \\ {0} & {\sigma_{a y}^{2}} \end{array}\right)$$

最终

$$Q = G Q_{\nu} G^{T} = \left(\begin{array}{cccc} {\frac{\Delta t^{4}}{4} \sigma_{a x}^{2}} & {0} & {\frac{\Delta t^{3}}{2} \sigma_{a x}^{2}} & {0} \\ {0} & {\frac{\Delta t^{4}}{4} \sigma_{a y}^{2}} & {0} & {\frac{\Delta t^{3}}{2} \sigma_{a y}^{2}} \\ {\frac{\Delta t^{3}}{2} \sigma_{a x}^{2}} & {0} & {\Delta t^{2} \sigma_{a x}^{2}} & {0} \\ {0} & {\frac{\Delta t^{3}}{2} \sigma_{a y}^{2}} & {0} & {\Delta t^{2} \sigma_{a y}^{2}} \end{array}\right)$$

Measurement Update

测量方程

$$z = h(x^{\prime}) + \omega$$

Lidar Measurements

Lidar测量方程

$$z = \left(\begin{array}{c}{p_{x}} \\ {p_{y}}\end{array}\right) = \left(\begin{array}{cccc} {1} & {0} & {0} & {0} \\ {0} & {1} & {0} & {0} \end{array}\right) \left(\begin{array}{c} {p_{x}^{\prime}} \\ {p_{y}^{\prime}} \\ {v_{x}^{\prime}} \\ {v_{y}^{\prime}} \end{array}\right)$$

简写为

$$z = H x^{\prime} + \omega \quad s.t. \quad \omega \sim N(0,R)$$

上式中的状态转移矩阵H，也即 Measurement Jacobian Matrix

$$H = \left(\begin{array}{cccc} {1} & {0} & {0} & {0} \\ {0} & {1} & {0} & {0} \end{array}\right)$$

Lidar Measurement Noise Covariance Matrix

$$R = E\left[\omega \omega^{T}\right] = \left(\begin{array}{cc} {\sigma_{p x}^{2}} & {0} \\ {0} & {\sigma_{p y}^{2}} \end{array}\right)$$

Radar Measurements

Radar测量方程

$$z = \left(\begin{array}{l} {\rho} \\ {\varphi} \\ {\dot{\rho}} \end{array}\right) = h(x^{\prime}) + \omega = \left(\begin{array}{c} {\sqrt{p_{x}^{\prime 2}+p_{y}^{\prime 2}}} \\ {\arctan \left(p_{y}^{\prime} / p_{x}^{\prime}\right)} \\ {\frac{p_{x}^{\prime} v_{x}^{\prime}+p_{y} v_{y}^{\prime}}{\sqrt{p_{x}^{\prime 2}+p_{y}^{\prime 2}}}} \end{array}\right) + \omega \quad s.t. \quad \omega \sim N(0,R)$$

• range $\rho$: the radial distance from the origin to our pedestrian
• bearing $\varphi$: the angle between the ray and x direction
• range rate $\dot{\rho}$: known as Doppler or radial velocity is the velocity along this ray

Measurement Jacobian Matrix

$$H = \left[\begin{array}{llll} {\frac{\partial \rho}{\partial p_{x}}} & {\frac{\partial \rho}{\partial p_{y}}} & {\frac{\partial \rho}{\partial v_{x}}} & {\frac{\partial \rho}{\partial v_{y}}} \\ {\frac{\partial \varphi}{\partial p_{x}}} & {\frac{\partial \varphi}{\partial p_{y}}} & {\frac{\partial \varphi}{\partial v_{x}}} & {\frac{\partial \varphi}{\partial v_{y}}} \\ {\frac{\partial \dot{\rho}}{\partial p_{x}}} & {\frac{\partial \rho}{\partial p_{y}}} & {\frac{\partial \dot{\rho}}{\partial v_{x}}} & {\frac{\partial \rho}{\partial v_{y}}} \end{array}\right] = \left[\begin{array}{cccc} {\frac{p_{x}}{\sqrt{p_{x}^{2}+p_{y}^{2}}}} & {\frac{p_{y}}{\sqrt{p_{x}^{2}+p_{y}^{2}}}} & {0} & {0} \\ {-\frac{p_{y}}{p_{x}^{2}+p_{y}^{2}}} & {\frac{p_{x}}{p_{x}^{2}+p_{y}^{2}}} & {0} & {0} \\ {\frac{p_{y}\left(v_{x} p_{y}-v_{y} p_{x}\right)}{\left(p_{x}^{2}+p_{y}^{2}\right)^{3 / 2}}} & {\frac{p_{x}\left(v_{y} p_{x}-v_{x} p_{y}\right)}{\left(p_{x}^{2}+p_{y}^{2}\right)^{3 / 2}}} & {\frac{p_{x}}{\sqrt{p_{x}^{2}+p_{y}^{2}}}} & {\frac{p_{y}}{\sqrt{p_{x}^{2}+p_{y}^{2}}}} \end{array}\right]$$

Radar Measurement Noise Covariance Matrix

$$R = \left(\begin{array}{ccc} {\sigma_{\rho}^{2}} & {0} & {0} \\ {0} & {\sigma_{\varphi}^{2}} & {0} \\ {0} & {0} & {\sigma_{\dot{\rho}}^{2}} \end{array}\right)$$

R 表示了测量值的不确定度，一般由传感器的厂家提供

Reference

• Self-Driving Car ND - Sensor Fusion - Extended Kalman Filters