Linear Algebra in a Nutshell

Matrix

厄米特矩阵

埃尔米特矩阵等于自己的 共轭转置

• 厄米特矩阵 $A^H = A$

  • 实对称矩阵 $A^T = A$

• 反厄米特矩阵 $A^H = -A$

  • 实反对称矩阵 $A^T = -A$

正规矩阵

$$A^H A = A A^H$$

• 酉矩阵 $A^H A = A A^H = I$
  • 正交矩阵 $A^T A = AA^T = I$
    • 特殊正交矩阵：$\det(A) = +1$，是一个旋转矩阵
      • Givens矩阵：$G(i,j,\theta)$
    • 瑕旋转矩阵：$\det(A) = -1$，瑕旋转是旋转加上镜射
      • Householder矩阵：$H = I - 2 uu^T$

正定与半正定矩阵

在线性代数里，正定矩阵(positive definite matrix)有时简称为 正定阵。

对任意的非零向量 $\boldsymbol{x}$ 恒有 二次型

$$f = \boldsymbol{x}^T \boldsymbol{A} \boldsymbol{x} > 0$$

则称 $f$ 为 正定二次型，对应的矩阵为 正定矩阵；若 $f \ge 0$，则 对应的矩阵为 半正定矩阵。

直观理解

令 $Y=MX$，则 $X^T Y > 0$，所以

$$cos(\theta) = \frac{X^T Y}{\|X\|\|Y\|} > 0$$

因此，从另一个角度，正定矩阵代表一个向量经过它的变化后的向量与其本身的夹角 小于90度

判别对称矩阵A的正定性

• 求出A的所有特征值
  • 若A的特征值均为正数，则A是正定的；若A的特征值均为负数，则A为负定的。
• 计算A的各阶顺序主子式
  • 若A的各阶顺序主子式均大于零，则A是正定的；若A的各阶顺序主子式中，奇数阶主子式为负，偶数阶为正，则A为负定的。

伴随矩阵

余子式

在n阶行列式D中划去任意选定的k行、k列后，余下的元素按原来顺序组成的n-k阶行列式M，称为 行列式D的k阶子式A的余子式。

A关于第i行第j列的余子式（记作 $M_{ij}$）是去掉A的第i行第j列之后得到的(n− 1)×(n− 1)矩阵的行列式。

代数余子式

如果k阶子式A在行列式D中的行和列的标号分别为i1，i2，…，ik和j1，j2，…，jk。则在A的余子式M前面添加符号 $(-1)^{\left(i{1}+i{2}+, \ldots,+i{k}\right)+\left(j{1}+j{2}+, \ldots,+j{k}\right)}$，所得到的n-k阶行列式，称为 行列式D的k阶子式A的代数余子式。

A的 (代数)余子矩阵 是一个n×n的矩阵C，使得其第i行第j列的元素是A关于第i行第j列的代数余子式：

$$\mathbf{C}_{i j}=(-1)^{i+j} M_{i j}$$

伴随矩阵（adjoint matrix）

A的 代数余子矩阵 的 转置矩阵，也就是说， A的伴随矩阵是一个n×n的矩阵（记作adj(A)），使得其第i 行第j 列的元素是A关于第j 行第i 列的代数余子式

$$\mathbf{A}^* = \operatorname{adj}(\mathbf{A})=\mathbf{C}^{T}$$

自伴随矩阵

$$\mathbf{A}^* = \mathbf{A}$$

在数学里，作用于一个有限维的内积空间，一个自伴算子(self-adjoint operator)等于自己的伴随算子；等价地说，表达自伴算子的矩阵是埃尔米特矩阵。埃尔米特矩阵等于自己的共轭转置。

可逆矩阵（非奇异矩阵）

$$\mathbf{A}^{-1} = \frac{1}{|\mathbf{A}|} \mathbf{A}^*$$

• 矩阵乘以可逆矩阵 秩不变，因为可逆矩阵可以表示为初等矩阵的乘积，而初等变换不改变矩阵的秩（左乘-行变换，右乘-列变换）

其他

• 对角阵：任意正规矩阵 都可以经过 正交变换 变成 对角矩阵

• 上（下）三角阵

矩阵变换

初等变换

• 初等变换只是不影响矩阵的秩，其他的特性都改变了。

• 对于计算矩阵的行列式，不能进行初等变换，但是可以做行列的进加减，不能乘以系数。

正交变换

Givens rotation（吉文斯旋转）

在数值线性代数中，吉文斯旋转（Givens rotation）是在两个坐标轴所展开的平面中的旋转。

吉文斯旋转 矩阵：

$$G(i, j, \theta)=\left[\begin{array}{ccccccc} 1 & \cdots & 0 & \cdots & 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & & \vdots & & \vdots \\ 0 & \cdots & c & \cdots & s & \cdots & 0 \\ \vdots & & \vdots & \ddots & \vdots & & \vdots \\ 0 & \cdots & -s & \cdots & c & \cdots & 0 \\ \vdots & & \vdots & & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & \cdots & 0 & \cdots & 1 \end{array}\right]$$ $$G \triangleq\left[\begin{array}{cc} \cos \phi & \sin \phi \\ -\sin \phi & \cos \phi \end{array}\right]$$

当一个吉文斯旋转矩阵 $G(i, j, \theta)$ 从左侧乘另一个矩阵 $A$ 的时候，$GA$ 只作用于 $A$ 的第 $i$ 和 $j$ 行。

$$\left[\begin{array}{cc} c & -s \\ s & c \end{array}\right]\left[\begin{array}{l} a \\ b \end{array}\right]=\left[\begin{array}{l} r \\ 0 \end{array}\right]$$

明确计算出 $\theta$ 是没有必要的。我们转而直接获取 c, s 和 r。一个明显的解是

$$\begin{aligned} &r \leftarrow \sqrt{a^{2}+b^{2}}\\ &c \leftarrow a / r\\ &s \leftarrow-b / r \end{aligned}$$

• Givens 旋转在数值线性代数中主要的用途是在向量或矩阵中介入零。例如，这种效果可用于计算矩阵的 QR分解。

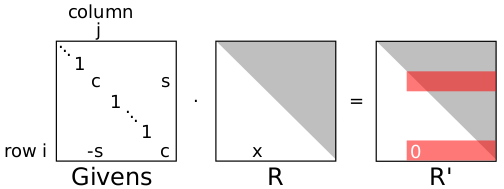
$$G_{j_{k}} \ldots G_{j_{2}} G_{j_{1}} R_{a}=\left[\begin{array}{c} R^{\prime} \\ 0 \end{array}\right]$$

• 超过 Householder变换 的一个好处是它们可以轻易的并行化，另一个好处是对于非常稀疏的矩阵计算量更小。

Eigen::Matrix<double, 5, 5> mat = Eigen::Matrix<double, 5, 5>::Random();
Eigen::JacobiRotation<double> temp_GR;
for (int n = 0; n < mat.cols(); ++n) {
  for (int m = (int)mat.rows() - 1; m > n; m--) {
    // Givens matrix G
    temp_GR.makeGivens(mat(m - 1, n), mat(m, n));
    (mat.block(m - 1, n, 2, mat.cols() - n)).applyOnTheLeft(0, 1, temp_GR.adjoint());
  }
}

Jacobi rotation

Householder 变换

豪斯霍尔德变换（Householder transformation）或译“豪斯霍德转换”，又称初等反射（Elementary reflection），这一变换将一个向量变换为由一个超平面反射的镜像，是一种线性变换。其变换矩阵被称作豪斯霍尔德矩阵，在一般内积空间中的类比被称作豪斯霍尔德算子。超平面的法向量被称作豪斯霍尔德向量。

豪斯霍尔德变换可以将向量的某些元素置零，同时保持该向量的范数不变。例如，将非零列向量 $\mathbf{x}=\left[x{1}, \dots, x{n}\right]^{T}$ 变换为单位基向量 $\mathbf{e}=[1,0, \ldots, 0]^{T}$ 的豪斯霍尔德矩阵为

$$\mathbf{H}=\mathbf{I}-\frac{2}{\langle\mathbf{v}, \mathbf{v}\rangle} \mathbf{v} \mathbf{v}^{H}$$

其中豪斯霍尔德向量 $\mathbf{v}$ 满足：

$$\mathbf{v}=\mathbf{x}+\operatorname{sgn}\left(\mathbf{x}_{1}\right)\|\mathbf{x}\|_{2} \mathbf{e}_{1}$$

Matrix Decomposition

EVD (Eigen Decomposition)

$$A = VDV^{-1}$$

• $A$ 是 方阵；$D$ 是 对角阵，其 特征值从大到小排列；$V$ 的列向量为 特征向量
• 若 $A$ 为 对称阵，则 $V$ 为 正交矩阵，其列向量为 $A$ 的 单位正交特征向量

SVD (Singular Value Decomposition)

• 谈谈矩阵的 SVD 分解

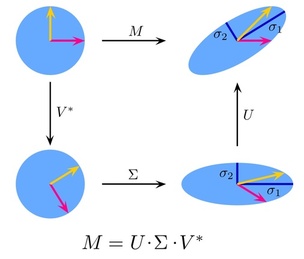
$$A = UDV^T$$

• $A$ 为 $m \times n$ 的矩阵；$D$ 是 非负对角阵，其 奇异值从大到小排列；$U$、$V$ 均为 正交矩阵

SVD分解十分强大且适用，因为任意一个矩阵都可以实现SVD分解，而特征值分解只能应用于方阵。

奇异值与特征值

$$AV = UD \Rightarrow Av_i = \sigma_{i} u_i \Rightarrow \sigma_{i} = \frac{Av_i}{u_i}$$ $$A^T A = (V D^T U^T) (U D V^T) = V D^2 V^T$$ $$A A^T = (U D V^T) (V D^T U^T) = U D^2 U^T$$

• $A^T A$ 的 特征向量 组成的是SVD中的 $V$ 矩阵
• $A A^T$ 的 特征向量 组成的是SVD中的 $U$ 矩阵
• $A^T A$ 或 $A A^T$ 的 特征值 $\lambda_i$ 与 $A$ 的 奇异值 $\sigma_i$ 满足 $\sigma_i = \sqrt{\lambda_i}$

PCA

奇异值减少得特别快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上，可以用 最大的 $k$ 个的奇异值和对应的左右奇异向量 来近似描述矩阵

$$A_{m \times n} = U_{m \times m} D_{m \times n} V_{n \times n}^T \approx U_{m \times k} D_{k \times k} V_{k \times n}^T$$

LU Decomposition

$$A = LU$$

• $A$ 是 方阵；$L$ 是 下三角矩阵；$U$ 是 上三角矩阵

PLU 分解

$$A = PLU$$

事实上，PLU 分解有很高的数值稳定性，因此实用上是很好用的工具。

LDU 分解

$$A = LDU$$

Cholesky Decomposition

• Cholesky decomposition

$$A = LDL^T$$

• $A$ 是 方阵，正定矩阵；$L$ 是 下三角矩阵

classic:

$$A = LL^T \\[2ex] A^{-1} = (L^T)^{-1} L^{-1} = (L^{-1})^T L^{-1}$$

LDLT

• LDLT for Checking Positive Semidefinite Matrix’s Singularity

QR Decomposition

• QR decomposition

$$A = QR$$

• $A$ 为 $m \times n$ 的矩阵；$Q$ 为 酉矩阵；$R$ 是 上三角矩阵

Four Fundamental Subspaces

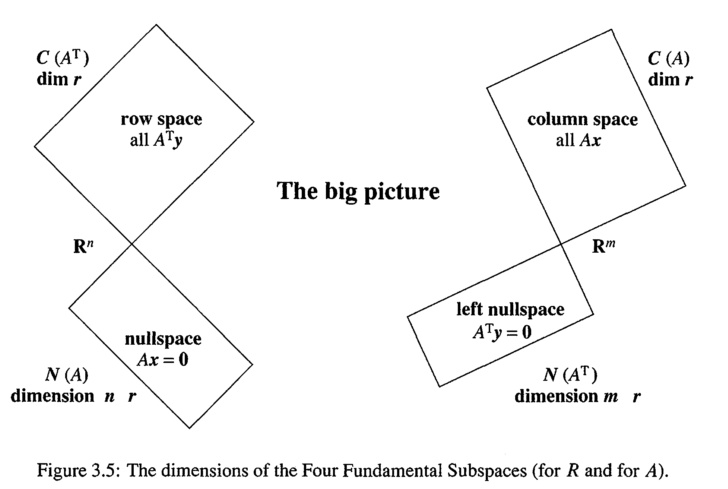
• 零空间 与 行空间 正交
• 左零空间 与 列空间 正交

column space (the range or image) $C(A)$

In linear algebra, the column space (also called the range or image) of a matrix A is the span (set of all possible linear combinations) of its column vectors. The column space of a matrix is the image or range of the corresponding matrix transformation.

row space $C(A^T)$

nullspace $N(A)$

$$A x = 0$$

The nullity of a matrix is the dimension of the null space.

The rank and nullity of a matrix A with n columns are related by the equation:

$$\operatorname{rank}(A) + \operatorname{nullity}(A) = n$$

left nullspace $N(A^T)$

$$A^T x = 0 \longrightarrow x^T A = 0$$

左零空间 求解

已知

$$A \in \mathbb{R}^{m \times n}, \quad \operatorname{rank}(A) = r = n, \quad m > n$$

SVD

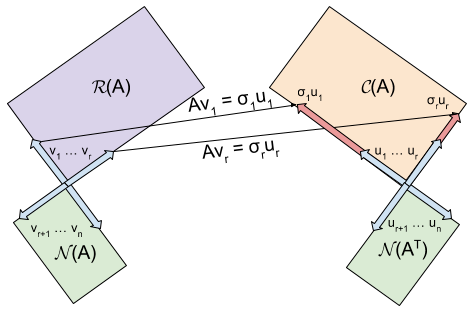
$$\begin{aligned} A_{m \times n} &= U_{m \times m} \cdot {\Sigma}_{m \times n} \cdot V_{n \times n}^T \\ &= \left[\begin{array}{ccc|ccc} u_{1} & \cdots & u_{r} & u_{r+1} & \cdots & u_{m} \end{array}\right] \left[\begin{array}{ccc|c} \sigma_{1} & & & \\ & \ddots & & 0 \\ & & \sigma_{r} & \\ \hline & 0 & & 0 \end{array}\right] \left[\begin{array}{c} v_{1}^{T} \\ \vdots \\ v_{r}^{T} \\ \hline v_{r+1}^{T} \\ \vdots \\ v_{n}^{T} \end{array}\right] \\ &= \begin{bmatrix} {U_1}_{m \times r} & {U_2}_{m \times (m-r)} \end{bmatrix} \cdot \begin{bmatrix} {\Sigma}_r & 0 \\ 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} {V_1}_{n \times r}^T \\[3pt] {V_2}_{n \times (n-r)}^T \end{bmatrix} \\ &= U_1 \cdot \Sigma_r \cdot V_1^T \\ &= \sum_{i=1}^r \sigma_i u_i v_i^T \end{aligned}$$

nullspace

$$A \cdot V_2 = 0 \longrightarrow N(A) = V_2 \in \mathbb{R}^{n \times (n-r)}$$

left nullspace

$$U_2^T \cdot A = 0 \longrightarrow N(A^T) = U_2 \in \mathbb{R}^{(m-r) \times m}$$

column space or the range (????)

$$C(A) = U_1^T \in \mathbb{R}^{r \times m}$$

QR

$$\begin{aligned} A_{m \times n} &= Q_{m \times m} \cdot R_{m \times n} \\ &= \begin{bmatrix} {Q_1}_{m \times r} & {Q_2}_{m \times (m-r)} \end{bmatrix} \begin{bmatrix} R_1 \\ 0 \end{bmatrix} \end{aligned}$$

left nullspace

$$Q_2^T \cdot A = 0 \longrightarrow N(A^T) = Q_2 \in \mathbb{R}^{(m-r) \times m}$$

线性方程组

非齐次线性方程组

$$A_{m \times n} x = b_{m \times 1}$$

在非齐次方程组中，A到底有没有解析解，可以由增广矩阵来判断：

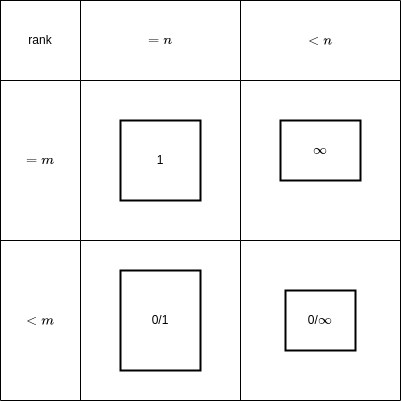
• r(A) > r(A | b) 不可能，因为增广矩阵的秩大于等于系数矩阵的秩
• r(A) < r(A | b) 方程组无解；
• r(A) = r(A | b) = n，方程组有唯一解；
• r(A) = r(A | b) < n，方程组无穷解；

非齐次线性方程组的最小二乘问题

$$x^* = \arg \min_x{\|Ax - b\|}_2^2$$

m个方程求解n个未知数，有三种情况：

• m=n
  • 且A为非奇异，则有唯一解 $x=A^{-1}b$
• m>n，超定问题（overdetermined）
  • $x=A^{+}b$
• m<n，欠定问题（underdetermined）

齐次线性方程组

$$A_{m \times n} x = 0$$

齐次线性方程 解空间维数=n-r(A)

• r(A) = n
  • A 是方阵，该方程组有唯一的零解
  • A 不是方阵(m>n)，解空间只含有零向量
• r(A) < n
  • 该齐次线性方程组有非零解，而且不唯一（自由度为n-r(A))

齐次线性方程组的最小二乘问题

$$\min{\|Ax\|}_2^2 \quad s.t. \quad \|x\| = 1$$

• 最小二乘解为 矩阵 $A^TA$ 最小特征值所对应的特征向量
• $\text{EVD}(A^{T}A)=[V,D]$，找最小特征值对应的V中的特征向量
• $\text{SVD}(A)=[U,S,V]$，找S中最小奇异值对应的V的右奇异向量

Solver

直接法

• Choleskey
• QR

迭代法

CG (Conjugate Gradient, 共轭梯度法)

PCG (Preconditioned Conjugate Gradient)

梯度下降法 vs 共轭梯度法

with Eigen

• Eigen 3.2稀疏矩阵入门

• Catalogue of dense decompositions

• Benchmark of dense decompositions

• Solving linear least squares systems

  • SVD decomposition (the most accurate but the slowest)
  • QR decomposition
  • normal equations (the fastest but least accurate)

• Solving Sparse Linear Systems