视觉SLAM位姿估计（总结）

[TOC]

相关代码：

• pose_estimation in cggos/slam_park_cg

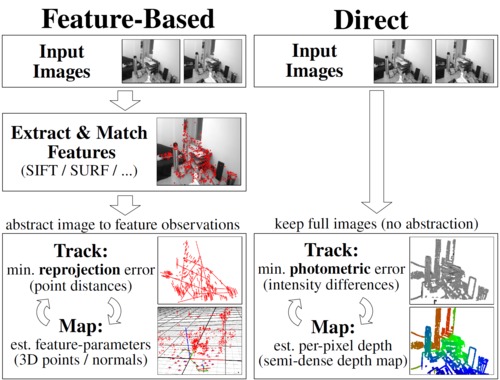
Features Based Method

2D-2D: Epipolar Geometry

2D-2D相机位姿估计 通常利用 对极几何 进行计算，是单目SLAM初始化时的关键技术。

2D-2D 对极几何 主要涉及到基础矩阵、本质矩阵和单应性矩阵的求解，并从中恢复出旋转矩阵 $R$ 和平移向量 $t$。

• 计算机视觉对极几何之FEH

同时，还要根据匹配的特征点和计算出的相对位姿进行三角化，恢复出 3D空间点。

• 计算机视觉对极几何之Triangulate(三角化)

在单目视觉SLAM中，以上过程主要用于SLAM的初始化：计算第二关键帧的相对位姿（假设第一帧位姿为 $[I \quad 0]$），并计算初始Map。

• 计算 基础矩阵或本质矩阵 适用于特征点不共面的情况，计算 单应矩阵 适用于特征点共面的情况

• 当 特征点共面 或者 相机发生纯旋转 时，基础矩阵 $F$ 的自由度下降，就会出现所谓的 退化(degenerate)。为了能够避免退化现象的影响，通常会 同时估计基础矩阵 $F$ 和 单应矩阵 $H$，选择重投影误差比较小的那个作为最终的运动估计矩阵。

• 平移向量t 的 尺度不确定性

• 初始化的纯旋转问题：单目初始化不能只有旋转，必须要有一定程度的平移，否则由于t趋近于0，导致无从求解R或者误差非常大
• 多于8对点：RANSAC

OpenCV 中相关函数：

• findFundamentalMat
• findEssentialMat
• findHomography
• recoverPose
• decomposeEssentialMat
• triangulatePoints

相关参考代码：

vector<Point2f> pts1;
vector<Point2f> pts2;
for ( int i = 0; i < ( int ) matches.size(); i++ ) {
    pts1.push_back(keypoints_1[matches[i].queryIdx].pt);
    pts2.push_back(keypoints_2[matches[i].trainIdx].pt);
}

Mat matF = findFundamentalMat(pts1, pts2, CV_FM_8POINT);

double cx = K.at<double>(0,2);
double cy = K.at<double>(1,2);
double fx = K.at<double>(0,0);
Mat matE = findEssentialMat(pts1, pts2, fx, Point2d(cx,cy));

Mat matH = findHomography(pts1, pts2, RANSAC, 3);

recoverPose(matE, pts1, pts2, R, t, fx, Point2d(cx,cy));

Ref: 2D-2D相机位姿估计

3D-2D: PnP

Perspective-n-Point is the problem of estimating the pose of a calibrated camera given a set of n 3D points in the world and their corresponding 2D projections in the image. [Wikipedia]

PnP(Perspective-n-Point) 是求解3D到2D点对运动的方法，求解PnP问题目前主要有直接线性变换（DLT）、P3P、EPnP、UPnP以及非线性优化方法。

在双目或RGB-D的视觉里程计中，可以直接使用PnP估计相机运动；而在单目视觉里程计中，必须先进行初始化，然后才能使用PnP。

在SLAM中，通常先使用 P3P或EPnP 等方法估计相机位姿，再构建最小二乘优化问题对估计值进行调整（BA）。

DLT

直接构建一个12个未知数的[R|t]增广矩阵（先不考虑旋转矩阵的自由度只有3），取六个点对，去求解12个未知数（每一个3D点到归一化平面的映射给出两个约束），最后将[R|t]左侧3x3矩阵块进行QR分解，用一个旋转矩阵去近似（将3x3矩阵空间投影到SE(3)流形上）。

P3P

通过3对3D/2D匹配点，得到A、B、C在相机坐标系下的3D坐标；然后，扥局3D-3D的点对，计算相机运动的R和t。

EPnP

需要4对不共面的（对于共面的情况只需要3对）3D-2D匹配点，是目前最有效的PnP求解方法。

Motion Only BA（非线性优化）

把 PnP问题 构建成一个定义于李代数上的非线性最小二乘问题，求解最好的相机位姿。

定义 残差（观测值-预测值）或 重投影误差

$$r(\xi) = u - K \exp({\xi}^{\wedge}) P$$

构建最小二乘问题

$${\xi}^* = \arg \min_\xi \frac{1}{2} \sum_{i=1}^{n} {\| r(\xi) \| }_2^2$$

细节可参考 应用: 基于李代数的视觉SLAM位姿优化

OpenCV 中相关函数：

• solvePnP
• Rodrigues

相关参考代码：

vector<KeyPoint> kpts_1, kpts_2;
vector<DMatch> matches;
find_feature_matches ( img_1, img_2, kpts_1, kpts_2, matches );

vector<Point3f> pts_3d;
vector<Point2f> pts_2d;
for ( DMatch m : matches ) {
    int x1 = int(kpts_1[m.queryIdx].pt.x);
    int y1 = int(kpts_1[m.queryIdx].pt.y);
    ushort d = img_d.ptr<unsigned short>(y1)[x1];
    if (d == 0)   // bad depth
        continue;
    float dd = d / depth_scale;

    Point2d p1 = pixel2cam(kpts_1[m.queryIdx].pt, K);

    pts_3d.push_back(Point3f(p1.x * dd, p1.y * dd, dd));
    pts_2d.push_back(kpts_2[m.trainIdx].pt);
}

Mat om, t;
solvePnP ( pts_3d, pts_2d, K, Mat(), om, t, false, SOLVEPNP_EPNP );
Mat R;
cv::Rodrigues ( om, R ); // rotation vector to rotation matrix

bundle_adjustment_3d2d ( pts_3d, pts_2d, K, R, t );

3D-3D: ICP

对于3D-3D的位姿估计问题可以用 ICP(Iterative Closest Point) 求解，其求解方式分为两种：

• 线性代数方式（主要是 SVD）
• 非线性优化方式（类似于BA）

线性代数方式

根据ICP问题，建立第 $i$ 对点的误差项

$$e_i = P_i - (R \cdot {P'}_i + t)$$

构建最小二乘问题，求使误差平方和达到极小的 $R, t$

$$\min_{R,t} J = \frac{1}{2} \sum_{i=1}^{n} {\| e_i \|}_2^2$$

对目标函数处理，最终为

$$\min_{R,t} J = \frac{1}{2} \sum_{i=1}^{n} ( {\| P_i - P_c - R({P'}_i-{P'}_c) \|}^2 + {\| P_c - R{P'}_c - t \|}^2 )$$

根据上式，可以先求解 $R$，再求解 $t$

1. 计算两组点的质心 $P_c$ 和 ${P’}_c$
2. 计算每个点的去质心坐标 $Q_i = P_i -P_c$ 和 ${Q’}_i = {P’}_i - {P’}_c$
3. 定义矩阵 $W = \sum_{i=1}^{n} Q_i {Q’}_i^T$，再SVD分解 $W = U {\Sigma} V^T$
4. 当 $W$ 满秩时， $R = UV^T \quad$
5. 计算 $t = P_c - R \cdot {P’}_c$

相关参考代码：

cv::Point3f p1, p2;
int N = pts1.size();
for (int i = 0; i < N; i++) {
    p1 += pts1[i];
    p2 += pts2[i];
}
p1 /= N;
p2 /= N;

std::vector<cv::Point3f> q1(N), q2(N);
for (int i = 0; i < N; i++) {
    q1[i] = pts1[i] - p1;
    q2[i] = pts2[i] - p2;
}

Eigen::Matrix3d W = Eigen::Matrix3d::Zero();
for (int i = 0; i < N; i++) {
    Eigen::Vector3d v3q1 = Eigen::Vector3d(q1[i].x, q1[i].y, q1[i].z);
    Eigen::Vector3d v3q2 = Eigen::Vector3d(q2[i].x, q2[i].y, q2[i].z);
    W += v3q1 * v3q2.transpose();
}

double determinantW =
 W(0,0)*W(1,1)*W(2,2) + W(0,1)*W(1,2)*W(2,0) + W(0,2)*W(1,0)*W(2,1) -
(W(0,0)*W(1,2)*W(2,1) + W(0,1)*W(1,0)*W(2,2) + W(0,2)*W(1,1)*W(2,0));

assert(determinantW>1e-8);

// SVD on W
Eigen::JacobiSVD<Eigen::Matrix3d> svd(W, Eigen::ComputeFullU | Eigen::ComputeFullV);
Eigen::Matrix3d U = svd.matrixU();
Eigen::Matrix3d V = svd.matrixV();

R = U * (V.transpose());
t = Eigen::Vector3d(p1.x, p1.y, p1.z) - R * Eigen::Vector3d(p2.x, p2.y, p2.z);

Optical Flow

光流是一种描述像素随时间在图像之间运动的方法，计算部分像素的称为 稀疏光流，计算所有像素的称为 稠密光流。稀疏光流以 Lucas-Kanade光流 为代表，并可以在SLAM中用于跟踪特征点位置。

LK光流

灰度不变假设

$$I(x+dx, y+dy, t+dt) = I(x, y, t)$$

对左边一阶泰勒展开

$$I(x+dx, y+dy, t+dt) = I(x, y, t) + \frac{\partial I}{\partial x} dx + \frac{\partial I}{\partial y} dy + \frac{\partial I}{\partial t} dt$$

则

$$\frac{\partial I}{\partial x} dx + \frac{\partial I}{\partial y} dy + \frac{\partial I}{\partial t} dt = 0$$

整理得

$$\frac{\partial I}{\partial x} \frac{dx}{dt} + \frac{\partial I}{\partial y} \frac{dy}{dt} = - \frac{\partial I}{dt}$$

简写为

$$I_x u + I_y v = -I_t$$

即

$$\begin{bmatrix} I_x & I_y \end{bmatrix} \begin{bmatrix} u \\ v \end{bmatrix} = -I_t$$

在LK光流中，假设某个窗口（w x w）内的像素具有相同的运动

$${\begin{bmatrix} I_x & I_y \end{bmatrix}}_k \begin{bmatrix} u \\ v \end{bmatrix} = -{I_t}_k, \quad k=1, \dots, w^2$$

简写为

$$J \begin{bmatrix} u \\ v \end{bmatrix} = -e$$

计算

$$J^T J \begin{bmatrix} u \\ v \end{bmatrix} = - J^T e$$

从而得到图像间的运动速度或者某块像素的位置。

分类

增量方式	Forward	Inverse
Additive	FAIA	IAFA
Compositional	FCIA	ICIA

Forward-Additive 光流:

$$\min_{\Delta x_i, \Delta y_i} \sum_{W} {\| I_1(x_i,y_i) - I_2(x_i+\Delta x_i, y_i+\Delta y_i) \|}_2^2$$

在迭代开始时，Gauss-Newton 的计算依赖于 $I_2$ 在 $(x_i, y_i)$ 处的梯度信息。然而，角点提取算法仅保证了 $I_1(x_i,y_i)$ 处是角点(可以认为角度点存在明显梯度)，但对于 $I_2$，我们并没有办法假设 $I_2$ 在 $(x_i,y_i)$ 处亦有梯度，从而 Gauss-Newton 并不一定成立。

反向的光流法(inverse) 则做了一个巧妙的技巧，即用 $I_1(x_i,y_i)$ 处的梯度，替换掉原本要计算的 $I_2(x_i+\Delta x_i, y_i+\Delta y_i)$ 的梯度。$I_1(x_i,y_i)$ 处的梯度不随迭代改变，所以只需计算一次，就可以在后续的迭代中一直使用，节省了大量计算时间。

讨论

• 在光流中，关键点的坐标值通常是浮点数，但图像数据都是以整数作为下标的。在光流中，通常的优化值都在几个像素内变化，所以用浮点数的像素插值（双线性插值）。
• 光流法通常只能估计几个像素内的误差。如果初始估计不够好，或者图像运动太大，光流法就无法得到有效的估计(不像特征点匹配那样)。但是，使用图像金字塔，可以让光流对图像运动不那么敏感。
• 多层金字塔光流

OpenCV 中相关函数：

• calcOpticalFlowPyrLK

相关参考代码：

for (int index = 0; index < count; index++) {
    color = colorImgs[index];
    depth = depthImgs[index];

    if (index == 0) {
        vector<cv::KeyPoint> kps;
        cv::Ptr<cv::FastFeatureDetector> detector =
         cv::FastFeatureDetector::create();
        detector->detect(color, kps);
        for (auto kp:kps)
            keypoints.push_back(kp.pt);
        last_color = color;
        continue;
    }
    if (color.data == nullptr || depth.data == nullptr)
        continue;

    vector<cv::Point2f> next_keypoints;
    vector<cv::Point2f> prev_keypoints;
    for (auto kp:keypoints)
        prev_keypoints.push_back(kp);

    vector<unsigned char> status;
    vector<float> error;
    cv::calcOpticalFlowPyrLK(
      last_color, color, prev_keypoints, next_keypoints, status, error);

    int i = 0;
    for (auto iter = keypoints.begin(); iter != keypoints.end(); i++) {
        if (status[i] == 0) {
            iter = keypoints.erase(iter);
            continue;
        }
        * iter = next_keypoints[i];
        iter++;
    }

    last_color = color;
}

Direct Method

根据使用像素的数量，直接法分为以下三种

• 稀疏直接法：使用稀疏关键点，不计算描述子
• 半稠密直接法：只使用带有梯度的像素点，舍弃像素梯度不明显的地方
• 稠密直接法：使用所有像素

利用直接法计算相机位姿，建立优化问题时，最小化的是 光度误差（Photometric Error）

$$r(\xi) = I_1(p) - I_2(p') = I_1(p) - I_2( K \exp({\xi}^{\wedge}) P )$$

构建最小二乘问题

$${\xi}^* = \arg \min_\xi \frac{1}{2} \sum_{i=1}^{n} {\| r(\xi) \| }_2^2$$

更具体地，稀疏直接法

$${\xi}^* = \arg \min_\xi \frac{1}{N} \sum_{i=1}^N \sum_{W_i} {\| I_1(p_i) - I_2 (\pi(\exp({\xi}^{\wedge}) \pi_{-1}(p_i))) \|}_2^2$$

其雅克比矩阵的计算，可参见 视觉SLAM位姿优化时误差函数雅克比矩阵的计算

相关参考代码：

bool pose_estimation_direct(
        const vector<Measurement>& measurements,
        cv::Mat* gray, Eigen::Matrix3f& K, Eigen::Isometry3d& Tcw) {

    typedef g2o::BlockSolver<g2o::BlockSolverTraits<6, 1>> DirectBlock;
    DirectBlock::LinearSolverType * linearSolver =
    new g2o::LinearSolverDense<DirectBlock::PoseMatrixType>();
    DirectBlock * solver_ptr = new DirectBlock(linearSolver);

    g2o::OptimizationAlgorithmLevenberg * solver =
    new g2o::OptimizationAlgorithmLevenberg(solver_ptr);

    g2o::SparseOptimizer optimizer;
    optimizer.setAlgorithm(solver);
    optimizer.setVerbose(true);

    g2o::VertexSE3Expmap * pose = new g2o::VertexSE3Expmap();
    pose->setEstimate(g2o::SE3Quat(Tcw.rotation(), Tcw.translation()));
    pose->setId(0);
    optimizer.addVertex(pose);

    int id = 1;
    for (Measurement m: measurements) {
        EdgeSE3ProjectDirect * edge =
          new EdgeSE3ProjectDirect(
            m.pos_world, K(0, 0), K(1, 1), K(0, 2), K(1, 2), gray);
        edge->setVertex(0, pose);
        edge->setMeasurement(m.grayscale);
        edge->setInformation(Eigen::Matrix<double, 1, 1>::Identity());
        edge->setId(id++);
        optimizer.addEdge(edge);
    }

    optimizer.initializeOptimization();
    optimizer.optimize(30);
    Tcw = pose->estimate();
}

参考文献

• 《视觉SLAM十四讲》
• Lucas-Kanade 20 Years On: A Unifying Framework
• 相机位姿求解问题？（知乎）